回廊识路

图划分软件Metis的使用

9/7/2020 科研

Metis

Metis是由Karypis Lab开发的一个具有强大功能的图划分软件包，可用于划分不规则图(graph)、网格(mesh)以及计算稀疏矩阵(Sparse Matrices)的Fill-Reducing Orderings。它提供了一组可以独立运行的命令行程序，同时也提供API方便集成到C/C++或Fortran程序中。

由于图划分问题np-hard性质带来的求解难度，Metis更新并不频繁（从1997年开始发布，最近一次更新是2013年3月，已经很是良心），其核心算法也不再是当前最优秀的，但并不妨碍它继续作为一个经典且稳定的第三方库在开源领域（如，国产开源CFD软件OneFLOW）中发挥重要作用。

在我当前的研究课题中一个子问题涉及到图划分，使用Metis的C/C++接口成功求解了该问题。本文主要记录一下Metis软件包的简单使用过程，更多内容请参考Karypis Lab官网 (opens new window)。

Update

[2021-03-22] GitHub项目默认使用vs2019(msvc_142)编译，请在LearnMetis/Lib/metis/lib/目录下找到对应版本的.lib文件，并修改对应的依赖项即可。

[2022-01-06] Github增加一个带权图划分示例。

# 0. 准备条件

  • VS2017 / VS2019

  • CMake 3.18（最新版）

# 1. 下载&安装

参考Win10 VS安装METIS (opens new window)和使用METIS软件包进行图划分 (opens new window)，这两篇博客文章已经介绍得很详细，按照步骤进行即可。有几点这里再强调一下：

  • 官方文件BUILD-Windows.txt中建议使用CMake 2.8，但CMake 2.8不支持vs2017，下载安装最新版本的CMake即可，建议使用Scoop (opens new window)安装。

  • 配置CMake编译选项时注意选择正确的编译器版本和机器位数，如本次实验中直接选择了vs2017 + release + x64。

  • 使用MSC编译器需要注释掉gk_arch.h文件中的一行代码，不要忘了。

  • 如果CMake配置的目标路径在C盘，可能需要使用管理员权限启动vs2017才能成功生成解决方案。

# 2. 在新项目中添加依赖

vs中引用第三方静态库永远都是关注两个文件(.h和.lib)、三个配置项：

  • 附加包含目录：.h文件所在的目录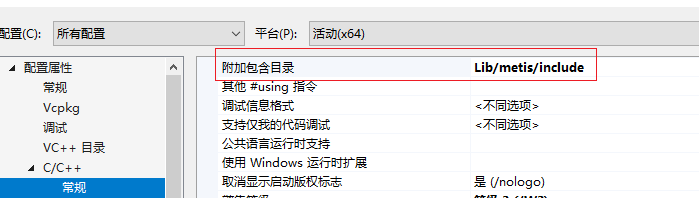

    附加包含目录

  • 附加库目录：.lib文件所在的目录

    附加库目录

  • 附加依赖项：.lib文件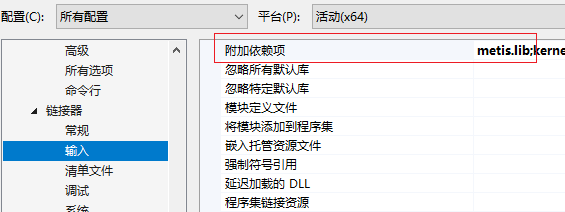

    附加依赖项

具体可以参考vs2017中lib的使用#项目配置。

PS

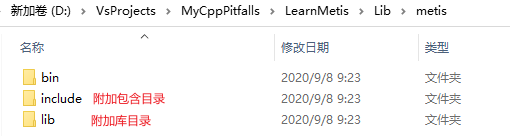
在新项目中建立Lib/目录，将用到的第三方库文件都复制到该目录，使用相对路径配置附加包含/库目录（如上述图中所示），避免使用绝对路径，这样可以方便项目在不同机器之间迁移和节约协同开发成本。如下图所示：

使用相对路径配置依赖项

# 3. Metis' API介绍

安装完Metis后可以在manual/目录下找到说明文档manual.pdf，其中介绍了命令行程序(Programs)和API的使用方法。这里主要对用于图划分的两个接口METIS_PartGraphRecursive和METIS_PartGraphKway作简单说明。

API

Metis提供了Recursive和Kway两种划分方式，分别基于multilevel recursive bisection和multilevel k-way partitioning实现。我们这里不关心其核心算法思路，仅关注其具体使用场景，下面这段话摘自官网的Discussions：

"This function(METIS_PartGraphKway) should be used to partition a graph into a large number of partitions(greater than 8). If a small number of partitions is desired, the METIS_PartGraphRecursive should be used instead, as it produces somewhat better partitions."

即求解划分子图数目较多时（官方建议划分8个以上子图）使用METIS_PartGraphKway，小规模划分使用METIS_PartGraphRecursive能获得质量更好的解，在后面的实验中也验证了这点。

此外，重点关注以下几个参数（更多参数信息请参考文档manual.pdf）：

  • nvtxs: 节点数目。

  • ncon: 节点权重维度，默认1。

  • xadj,adjncy: Metis使用压缩图(CSR)表示图的邻接关系，详情参考文档Metis' API/Graph data structure部分。

  • vwgt: 节点权重列表，设为NULL表示节点无权重或所有节点权重相同，相当于按照子图中节点的数目平衡划分。

  • adjwgt: 边的权重列表，默认优化目标为切断边的权重之和最小，设为NULL则表示按照切边数最小划分。

  • nparts: 要划分的子图数目。

  • objval: 目标函数值。

  • part: 保存划分结果。

# 4. Demo

PS

Demo使用了manual.pdf中的一个简单带权算例，怎样在VS中用C++调用METIS提供的API (opens new window)和使用METIS软件包进行图划分 (opens new window)两篇博客文章中也使用了同样的算例。但通过我个人的学习与理解，认为他们在调用API时出现了明显的失误并已经在各自文章的评论区出指出了问题，如果我的理解有误，欢迎批评指正。

  • 算例图示及文件格式

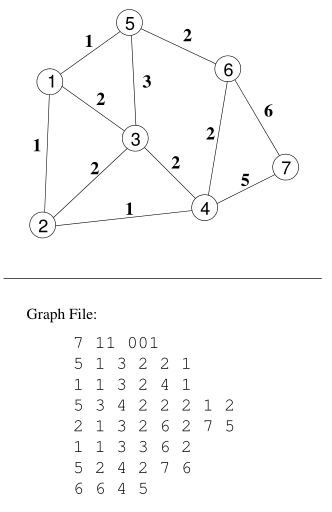
    算例图示及文件格式

  • 代码

#include <metis.h>
#include <vector>
#include <iostream>
#include <fstream>
#include <string>
#include <sstream>

using namespace std;

vector<idx_t> func(vector<idx_t> &xadj, vector<idx_t> &adjncy, vector<idx_t> &adjwgt, decltype(METIS_PartGraphKway) *METIS_PartGraphFunc) {
  idx_t nVertices = xadj.size() - 1; // 节点数
  idx_t nEdges = adjncy.size() / 2;  // 边数
  idx_t nWeights = 1;                // 节点权重维数
  idx_t nParts = 2;                  // 子图个数≥2
  idx_t objval;                      // 目标函数值
  vector<idx_t> part(nVertices, 0);  // 划分结果

  int ret = METIS_PartGraphFunc(&nVertices, &nWeights, xadj.data(), adjncy.data(),
    NULL, NULL, adjwgt.data(), &nParts, NULL,
    NULL, NULL, &objval, part.data());

  if (ret != rstatus_et::METIS_OK) { cout << "METIS_ERROR" << endl; }
  cout << "METIS_OK" << endl;
  cout << "objval: " << objval << endl;
  for (unsigned part_i = 0; part_i < part.size(); part_i++) {
    cout << part_i + 1 << " " << part[part_i] << endl;
  }

  return part;
}

int main() {
  ifstream ingraph("graph.txt");

  int vexnum, edgenum;
  string line;
  getline(ingraph, line);
  istringstream tmp(line);
  tmp >> vexnum >> edgenum;
  vector<idx_t> xadj(0);
  vector<idx_t> adjncy(0); // 压缩图表示
  vector<idx_t> adjwgt(0); // 边权重

  idx_t a, w;
  for (int i = 0; i < vexnum; i++) {
    xadj.push_back(adjncy.size());
    getline(ingraph, line);
    istringstream tmp(line);
    while (tmp >> a >> w) {
      adjncy.push_back(a - 1); // 节点id从0开始
      adjwgt.push_back(w);
    }
  }
  xadj.push_back(adjncy.size());
  ingraph.close();

  vector<idx_t> part = func(xadj, adjncy, adjwgt, METIS_PartGraphRecursive);
  //vector<idx_t> part = func(xadj, adjncy, adjwgt, METIS_PartGraphKway);

  ofstream outpartition("partition.txt");
  for (int i = 0; i < part.size(); i++) { outpartition << i + 1 << " " << part[i] << endl; }
  outpartition.close();

  return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

  • 运行结果

    • METIS_PartGraphRecursive划分结果：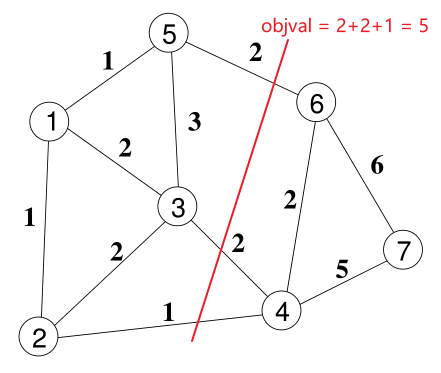

      recursive_result

    • METIS_PartGraphKway划分结果：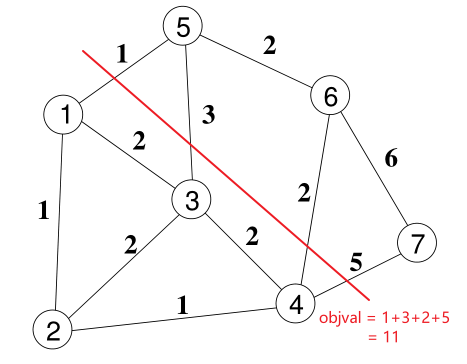

      kway_result

    可以看出，对于上述仅划分两个子图的情况，METIS_PartGraphRecursive要优于METIS_PartGraphKway；但在我的研究课题中，算例规模和子图数目稍大一些，经过测试使用METIS_PartGraphKway求解的质量更好。

PS

在实际使用过程中，可能会由于算例规模的变化交替使用两种划分办法。由于这两个API参数与返回值形式完全一致，建议使用传递函数指针的方式区分调用，避免写出大量重复代码。

# Github

项目实例均在vs2017/vs2019上测试，并上传至GitHub (opens new window)，将LearnMetis设为启动项目即可复现实验结果。

# Reference

Win10 VS安装METIS (opens new window)

怎样在VS中用C++调用METIS提供的API (opens new window)

使用METIS软件包进行图划分 (opens new window)

win10+vs2019从源代码编译网格剖分软件Metis5.1.0 (opens new window)