优先队列101

优先队列101

优先队列是堆这种数据结构的重要应用之一，甚至大多数语意下它俩指的就是同一个东西。但某些特殊情况下，STL自带的优先队列priority_queue并不能完全满足需求，比如查找/修改队列中的某个元素的优先级。本文介绍三种不同形式的优先队列，对处理这些特殊情况会有效果。

By the way...

要清晰地区分容器和容器适配器两个概念。容器适配器是对容器的上层封装，比如stack、queue都是由vector/deque适配实现。但容器适配器为了维护自己的数据结构特性，会阉割容器的部分原生接口，比如封闭一端的出入口、不支持随机访问、不提供迭代器遍历等。但少数情况下，我们确实需要“不完全符合规范”的数据结构。

写在前面……

本文将使用三种形式的优先队列实现堆优化版本的Dijkstra算法，数据结构定义如下：

#define INF 0x3f3f3f3f

#include <iostream>
#include <vector>
#include <queue>
#include <set>
#include <functional>

using std::vector;
using std::cout;
using std::endl;

struct Vertex { // 节点
	int id;
	int dist; // 距起点的距离

	Vertex() : id(-1), dist(INF) {}
	Vertex(int i, int d) : id(i), dist(d) {}
	bool operator<(const Vertex& rhs) const {
		if (dist == rhs.dist) return id < rhs.id;
		return dist < rhs.dist;
	}
};

struct Edge { // 边
	int sid;
	int tid;
	int w;

	Edge(int s, int t, int w) : sid(s), tid(t), w(w) {}
};

using AdjList = vector<vector<Edge>>;

class Graph {
public:
	Graph(int v) : v_num(v), dist(v_num, INF), adj(v_num) {}

	void add_edge(int s, int t, int w) { adj[s].emplace_back(s, t, w); }

	void dijkstraWithSTLQueue(int s, int t);

	void dijkstraWithSTLSet(int s, int t);

	void dijkstraWithCusQueue(int s, int t);

	void print_path(int s, int t, vector<int>& predecessor) {
		if (s == t) {
			cout << s;
			return;
		}
		print_path(s, predecessor[t], predecessor);
		cout << "->" << t;
	}

	void print_dist(int s, int t, vector<int>& dist) {
		cout << endl << s << "->" << t << ": " << dist[t] << endl;
	}

private:
	int v_num;
	vector<int> dist; // 距起点的最短路径
	AdjList adj;
};

1. priority_queue

STL中的priority_queue也是一种容器适配器，可以适配vector/deque，基于堆化操作make_heap实现。由于默认是大顶堆（优先级大的先出队），因此我们需要自定义比较函数，使最短路径先出队。

std::function<bool(const Vertex&, const Vertex&)> comp1 = [](const Vertex& lhs, const Vertex& rhs) {
	if (lhs.dist == rhs.dist) return lhs.id > rhs.id;
	return lhs.dist > rhs.dist; // STL priority_queue 默认大顶堆，需要传入自定义比较函数
};
using PriorityQueue1 = std::priority_queue<Vertex, std::vector<Vertex>, decltype(comp1)>;

算法实现

void dijkstraWithSTLQueue(int s, int t) {
    vector<int> predecessor(v_num);
    dist.clear();
    dist.resize(v_num, INF);
    dist[s] = 0;
    PriorityQueue1 q(comp1); // 小顶堆
    q.emplace(s, 0);
    while (!q.empty()) {
        auto curr = q.top();
        q.pop();
        if (curr.id == t) { break; } // 最短路径！
        for (auto& e : adj[curr.id]) {
            if (curr.dist + e.w < dist[e.tid]) {
                predecessor[e.tid] = curr.id; // 记录前驱节点
                dist[e.tid] = curr.dist + e.w;
                q.emplace(e.tid, dist[e.tid]);
            }
        }
    }
    print_path(s, t, predecessor);
    print_dist(s, t, dist);
    cout << "priority_queue队列中剩余元素: " << q.size() << endl;
}

算法分析

• 如果模拟节点出入队的过程会发现，存在同一节点重复入队的情况，但最终结果也是正确的，因为堆的特性保证了短路径一定会在长路径之前出队。算法终止的时候队列中会剩余重复入队元素，它们一定不是最短路，因此直接忽略，这就是所谓“延迟删除”（lazy deletion）技术。延迟删除技术可以看作是一种实现技巧，也可以理解成无法修改元素优先级时一种无奈的折中选择。
• 由于允许重复元素入队，队列的大小可能会达到E，因此基于优先队列+延迟删除技术的Dijkstra算法时间复杂度是O(E*logE)。如果是稀疏图的话，E ≤ V²意味着logE ≤ 2logV，因此算法的时间复杂度是O(E*logV)，这也说明实践中使用优先队列解决稀疏图的最短路径问题的有效性。
• 个人感觉STL默认大顶堆的设计有点反人类，如果是小顶堆的话，priority_queue与下文提到的set共用Vertex的<运算符即可，这样仅需写一个重载函数，而不需要定义两个完全不一样的比较函数。

2. set

set是STL自带的一种有序容器，基于红黑树实现，查找性能好，可以当作支持删除指定元素的优先队列使用。它要求元素支持比较，因此也需要实现比较函数。

auto comp2 = [](auto& lhs, auto& rhs) {
	if (lhs.dist == rhs.dist) return lhs.id < rhs.id;
	return lhs.dist < rhs.dist;
};
using PriorityQueue2 = std::set<Vertex, decltype(comp2)>;

//using PriorityQueue2 = std::set<Vertex>; // Vertex重载`<`运算符

注意

如果是自定义结构体要支持比较，需特别注意：set对于容器中元素的相等判定是!comp(a,b) && !comp(b,a)。比如这里不能只写一句return lhs.dist < rhs.dist就完事，这样dist相同id不同的节点是不会入队的。

算法实现

void dijkstraWithSTLSet(int s, int t) {
	vector<int> predecessor(v_num);
	dist.clear();
	dist.resize(v_num, INF);
	dist[s] = 0;
	PriorityQueue2 q(comp2);
	q.emplace(s, 0);
	while (!q.empty()) {
		auto curr = *q.begin(); // 当前最短路径出队并删除
		q.erase(q.begin());
		if (curr.id == t) { break; } // 最短路径！
		for (auto& e : adj[curr.id]) {
			if (curr.dist + e.w < dist[e.tid]) {
				predecessor[e.tid] = curr.id; // 记录前驱节点
				dist[e.tid] = curr.dist + e.w;
				for (auto iter = q.begin(); iter != q.end(); ++iter) {
					if (iter->id == e.tid) { // 如果在队列中则删除旧值
						q.erase(iter);
						break;
					}
				}
				q.emplace(e.tid, dist[e.tid]); // 新值入队
			}
		}
	}
	print_path(s, t, predecessor);
	print_dist(s, t, dist);
	cout << "set队列中剩余元素: " << q.size() << endl;
}

算法分析

• 可以看到，将set当作优先队列使用可以避免元素重复入队，使得队列中元素个数不会超过V。
• 红黑树插入、删除、查找的时间复杂度都是O(logn)，然而这里是无法用find函数以O(logV)的复杂度查询到对应元素的（还记得上文中提到的set是怎么判定相等元素的吗？）。好在set提供了迭代器遍历，使我们能以O(V)的复杂度查询元素，然后以O(logV)的复杂度删除它。综合下来，整个算法的时间复杂度是O(E*(V+logV)) = O(E*V)，反而上升了，有点舍近求远的感觉。
• 为了避免每次查询都耗费O(V)的时间复杂度，我们可以引入一个visited[]布尔数组提速，下文会用到。

3. 自定义优先队列

自己实现一个支持更新指定元素的小顶堆，其中add和poll操作时间复杂度是O(logn)，update操作的时间复杂度是O(n)（O(n)的时间查找+O(logn)的时间调整堆）。

class PriorityQueue3 {
public:
	PriorityQueue3(int c) : capacity(c), count(0) {
		nodes.resize(capacity + 1);
	}

	void add(Vertex&& data) {
		if (count >= capacity) return;
		++count;
		nodes[count] = data;
		heapify_float(count);
	}

	Vertex poll() {
		if (count == 0) return {};
		Vertex top = nodes[1];
		nodes[1] = nodes[count];
		--count;
		heapify_sink(1);
		return top;
	}

	void update(Vertex&& data) {
		int i = 1;
		for (; i <= count; ++i) {
			if (nodes[i].id == data.id) { break; }
		}
		if (nodes[i].dist > data.dist) {
			nodes[i].dist = data.dist;
			heapify_float(i); // 小的上浮
		}
		else {
			nodes[i].dist = data.dist;
			heapify_sink(i); // 大的下沉
		}
	}

	bool empty() const { return count == 0; }

	int size() const { return count; }

private:
	// 自下往上建堆，小的上浮
	void heapify_float(int i) {
		while (i / 2 > 0 && nodes[i].dist < nodes[i / 2].dist) {
			std::swap(nodes[i], nodes[i / 2]);
			i /= 2;
		}
	}

	// 自上往下堆化，大的下沉
	void heapify_sink(int i) {
		while (true) {
			int min_pos = i;
			if (i * 2 <= count && nodes[i * 2].dist < nodes[min_pos].dist) min_pos = i * 2;
			if (i * 2 + 1 <= count && nodes[i * 2 + 1].dist < nodes[min_pos].dist) min_pos = i * 2 + 1;
			if (min_pos == i) break;
			std::swap(nodes[min_pos], nodes[i]);
			i = min_pos;
		}
	}

private:
	std::vector<Vertex> nodes;
	int capacity;
	int count;
};

算法实现

	void dijkstraWithCusQueue(int s, int t) {
		vector<int> predecessor(v_num);
		dist.clear();
		dist.resize(v_num, INF);
		dist[s] = 0;
		PriorityQueue3 q(v_num);
		q.add({ s, 0 });
		vector<bool> visited(v_num, false);
		visited[s] = true; // 标记是否在队列中
		while (!q.empty()) {
			auto curr = q.poll();
			if (curr.id == t) { break; } // 最短路径！
			for (auto& e : adj[curr.id]) {
				if (dist[curr.id] + e.w < dist[e.tid]) {
					predecessor[e.tid] = curr.id;
					dist[e.tid] = dist[curr.id] + e.w;
					if (visited[e.tid]) {
						q.update({ e.tid, dist[e.tid] }); // 如果在队列中则更新dist值
					}
					else {
						q.add({ e.tid, dist[e.tid] });
						visited[e.tid] = true;
					}
				}
			}
		}
		print_path(s, t, predecessor);
		print_dist(s, t, dist);
		cout << "自定义优先队列中剩余元素: " << q.size() << endl;
	}

算法分析

• 自定义优先队列有点像是结合了priority_queue和set两种方法，它是基于堆实现的，但由于update操作涉及查询，时间复杂度降为O(V)。
• 为了避免无用的查询耗时，引入visited[]布尔数组标记元素是否在队列中。只有当元素在队列中时才会触发update查询，否则元素直接入队即可；另外只有dist小的元素才会更新，因此update调整堆时只会执行heapify_float操作。
• 最好时间复杂度是O(E*logV)，最差是O(E*V)，不妨写作O(E*(αV+βlogV)), α+β=1，其中α和β表示update和add操作的概率（其实是我不会分析了，留个坑，不填 ¯\(ツ)/¯ 。。。）。相关文章中作者直接把这种写法时间复杂度记为O(E*logV)，我觉得也没啥问题。

4. 小结

实验结果如下图所示：

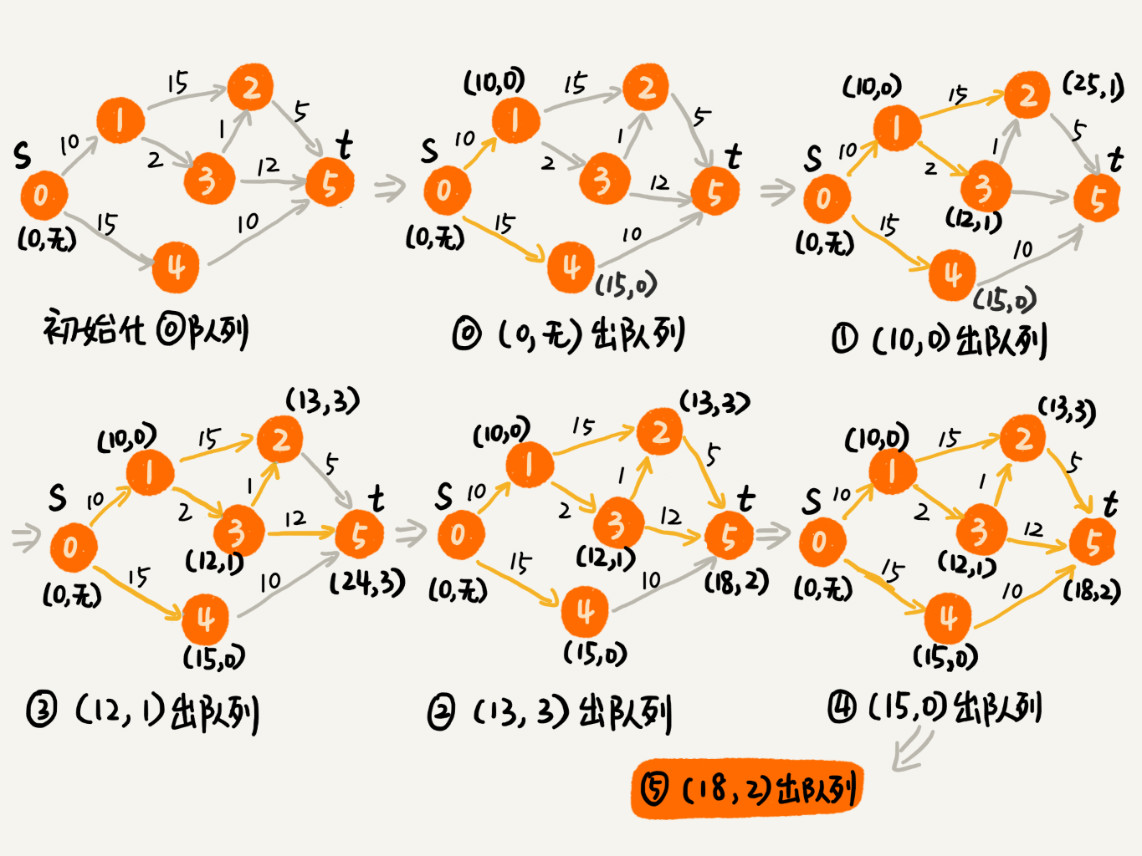
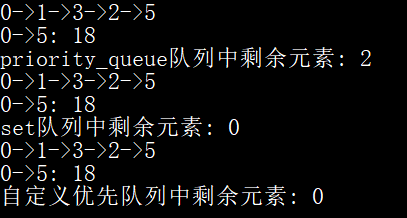
• 非优化版本的Dijkstra算法时间复杂度是O(V²)；

• 优先队列+延迟删除的时间复杂度是O(E*logE)，对于稀疏图是O(E*logV)，队列大小是边的数目E；

• 自定义支持更新的优先队列，算法的时间复杂度是O(E*logV)，队列大小是节点数目V；

• 直接使用STL自带的priority_queue是最方便的做法，也是首选方案；

• 专门为dijkstra算法设计的斐波那契堆是理论上最快的；

• 红黑树和堆的性能差距，暂时留坑，请参考CSDN | 红黑树 vs 最小堆 (opens new window)。

[Github] 代码

项目实例均在vs2019上测试，并上传至GitHub (opens new window)。

[Reference] 参考

极客时间 | 数据结构与算法之美 (opens new window)

CSDN | 红黑树 vs 最小堆 (opens new window)